Content:
- Introduction
- Parameterized generation
- Pythia6
- HIJING
- Additional universal generators
- Generators for specific studies
- Combination of generators: AliGenCocktail
Introduction
Heavy-ion collisions produce a very large number of particles in the final state. This is a challenge for the reconstruction and analysis algorithms. The development of these algorithms requires a predictive and precise simulation of the detector response. Model predictions discussed in the first volume of the Physics Performance Report for the charged multiplicity at LHC in Pb–Pb collisions vary from 1400 to 8000 particles in the central unit of rapidity. The experiment was designed when the highest nucleon–nucleon center-of-mass energy heavy-ion interactions was at 20 GeV per nucleon–nucleon pair at CERN SPS, i.e. a factor of about 300 less than the energy at LHC. RHIC at its top energy of 200 GeV per nucleon–nucleon pair is still 30 times less than the LHC energy. The RHIC data seem to suggest that the LHC multiplicity will be on the lower side of the interval. However, the extrapolation is so large that both the hardware and software of ALICE has been designed for the highest multiplicity. Moreover, as the predictions of different generators of heavy-ion collisions differ substantially at LHC energies, we have to use several of them and compare the results.
The simulation of the particles emerging from the interaction is confronted with several problems:
- Existing event generators give different answers on parameters such as expected multiplicities, p T -dependence and rapidity dependence at LHC energies.
- Most of the physics signals, like hyperon production, high-p T phenomena, open charm and beauty, quarkonia etc., are not exactly reproduced by the existing event generators.
- Simulation of small cross-sections would demand prohibitively long runs to simulate a number of events that is commensurable with the expected number of detected events in the experiment.
- The existing generators do not provide for event topologies like momentum correlations, azimuthal flow etc.
To allow nevertheless efficient simulations we have adopted a framework that allows for a number of options:
- The simulation framework provides an interface to external generators, like HIJING and DPMJET.
- A parameterized, signal-free, underlying event where the produced multiplicity can be specified as an input parameter is provided.
- Rare signals can be generated using the interface to external generators like PYTHIA or simple parameterizations of transverse momentum and rapidity spectra defined in function libraries.
- The framework provides a tool to assemble events from different signal generators (event cocktails).
- The framework provides tools to combine underlying events and signal events at the primary particle level (cocktail) and at the summable digit level (merging).
- Afterburners are used to introduce particle correlations in a controlled way. An afterburner is a program which changes the momenta of the particles produced by another generator, and thus modifies the multi-particle momentum distributions, as desired.
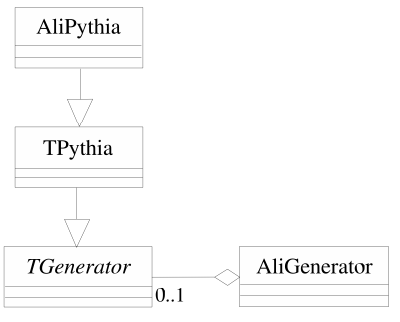
Generator objects have the task to produce particles that are put on the stack before tracking of an event is started. These particles can be final state particles or their parents (grandparents, ...). Final states particle will be transported and parent information is retained to be used in the analysis after transport. Generators generate particle type, particle kinematics and the statistical weight of the particles as well as their vertices. The user should be able to "bias" part or all of these variables in order to optimize computing time. For the simulation of physics processes the generator should keep track of the user bias. Generators differ by their sources (random numbers, parameterisations, external file, external MC generator ...).
AliGenerator is the base class, which has the responsibility to generate the primary particles of an event. Some realizations of this class do not generate the particles themselves but delegate the task to an external generator like PYTHIA through the TGenerator interface.
Parameterized generation
The event generation based on parameterization can be used to produce signal-free final states. It avoids the dependences on a specific model, and is efficient and flexible. It can be used to study the track reconstruction efficiency as a function of the initial multiplicity and occupancy.
AliGenHIJINGparam is an example of an internal AliRoot generator, based on parameterized pseudorapidity density and transverse momentum distributions of charged and neutral pions and kaons. The pseudorapidity distribution was obtained from a HIJING simulation of central PbPb collisions and scaled to a charged-particle multiplicity of 8000 in the pseudo rapidity interval | eta|<0.5. Note that this is about 10% higher than the corresponding value for a rapidity density with an average dN dy of 8.000 in the interval | y|<0.5. The transverse-momentum distribution is parameterized from the measured CDF pion p t-distribution at s 1/2=1.8 TeV . The corresponding kaon p t- distribution was obtained from the pion distribution by m t-scaling.
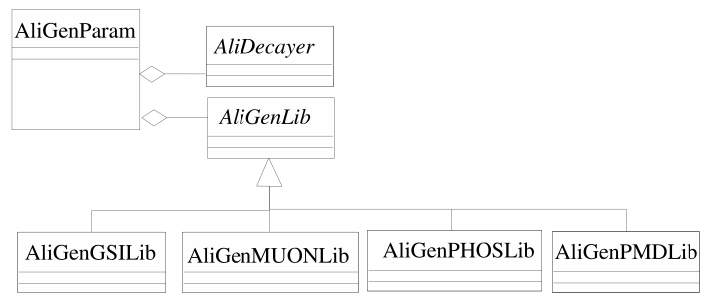
In many cases, the expected transverse momentum and rapidity distributions of particles are known. In other cases, the effect of variations in these distributions must be investigated. In both situations, it is appropriate to use generators that produce primary particles and their decays sampling from parameterized spectra. To meet the different physics requirements in a modular way, the parameterizations are stored in independent function libraries wrapped into classes that can be plugged into the generator.This is schematically illustrated in the following picture, where four different generator libraries can be loaded via the abstract generator interface.
An example of AliGenParam usage is presented below:
// Example for J/psi Production from Parameterization
// using default library (AliMUONlib)
AliGenParam *gener = new AliGenParam(ntracks, AliGenMUONlib::kUpsilon);
gener->SetMomentumRange(0,999); // Wide cut on the Upsilon momentum
gener->SetPtRange(0,999); // Wide cut on Pt
gener->SetPhiRange(0. , 360.); // Full azimutal range
gener->SetYRange(2.5, 4); // In the acceptance of the MUON arm
gener->SetCutOnChild(1); // Enable cuts on Upsilon decay products
gener->SetChildThetaRange(2,9); // Theta range for the decay products
gener->SetOrigin(0,0,0); // Vertex position
gener->SetSigma(0,0,5.3); // Sigma in (X,Y,Z) (cm) on IP position
gener->SetForceDecay(kDiMuon); // Upsilon->mu+ mu- decay
gener->SetTrackingFlag(0); // No particle transport
gener->Init();
Several event generators are available via the abstract ROOT class that implements the generic generator interface, TGenerator. By means of implementations of this abstract base class, we wrap FORTRAN Monte Carlo codes like PYTHIA, HERWIG, and HIJING that are thus accessible from the AliRoot classes. In particular the interface to PYTHIA includes the use of nuclear structure functions of LHAPDF.
Pythia6
Pythia is used for simulation of proton-proton interactions and for generation of jets in case of event merging. An example of minimum bias Pythia events is presented below:
AliGenPythia *gener = new AliGenPythia(-1);
gener->SetMomentumRange(0,999999);
gener->SetThetaRange(0., 180.);
gener->SetYRange(-12,12);
gener->SetPtRange(0,1000);
gener->SetProcess(kPyMb); // Min. bias events
gener->SetEnergyCMS(14000.); // LHC energy
gener->SetOrigin(0, 0, 0); // Vertex position
gener->SetSigma(0, 0, 5.3); // Sigma in (X,Y,Z) (cm) on IP position
gener->SetCutVertexZ(1.); // Truncate at 1 sigma
gener->SetVertexSmear(kPerEvent); // Smear per event
gener->SetTrackingFlag(1); // Particle transport
gener->Init();
HIJING
HIJING (Heavy-Ion Jet Interaction Generator) combines a QCD-inspired model of jet production using the Lund model for jet fragmentation. Hard or semi-hard parton scatterings with transverse momenta of a few GeV are expected to dominate high-energy heavy-ion collisions. The HIJING model has been developed with special emphasis on the role of mini jets in p-p, p-A and A-A reactions at collider energies.
Detailed systematic comparisons of HIJING results with a wide range of data demonstrate a qualitative understanding of the interplay between soft string dynamics and hard QCD interactions. In particular, HIJING reproduces many inclusive spectra, two-particle correlations, as well as the observed flavour and multiplicity dependence of the average transverse momentum.
The Lund FRITIOF model and the Dual Parton Model (DPM) have guided the formulation of HIJING for soft nucleusnucleus reactions at intermediate energies: (NN) 1/2 ; 20 GeV . The hadronic-collision model has been inspired by the successful implementation of perturbative QCD processes in PYTHIA. Binary scattering with Glauber geometry for multiple interactions are used to extrapolate to pA and AA collisions.
Two important features of HIJING are jet quenching and nuclear shadowing. Under jet quenching, we understand the energy of partons in nuclear matter. It is responsible for an increase of the particle multiplicity at central rapidities. Jet quenching is taken into account by an expected energy loss of partons traversing dense matter. A simple colour configuration is assumed for the multi-jet system and the Lund fragmentation model is used for the hadroniation. HIJING does not simulate secondary interactions.
Shadowing describes the modification of the free nucleon parton density in the nucleus. At low-momentum fractions, x, observed by collisions at the LHC, shadowing results in a decrease of multiplicity. Parton shadowing is taken into account using a parameterization of the modification.
Here is an example of event generation with HIJING:
AliGenHijing *gener = new AliGenHijing(-1);
gener->SetEnergyCMS(5500.); // center of mass energy
gener->SetReferenceFrame("CMS"); // reference frame
gener->SetProjectile("A", 208, 82); // projectile
gener->SetTarget ("A", 208, 82); // projectile
gener->KeepFullEvent(); // HIJING will keep the full parent child chain
gener->SetJetQuenching(1); // enable jet quenching
gener->SetShadowing(1); // enable shadowing
gener->SetDecaysOff(1); // neutral pion and heavy particle decays switched off
gener->SetSpectators(0); // Don't track spectators
gener->SetSelectAll(0); // kinematic selection
gener->SetImpactParameterRange(0., 5.); // Impact parameter range (fm)
gener->Init();
Additional universal generators
The following universal generators are available in AliRoot:
- AliGenDPMjet: this is an implementation of the dual parton model
- AliGenIsajet: a Monte Carlo event generator for pp, p p, and e e
- AliGenHerwig: Monte Carlo package for simulating Hadron Emission Reactions With Interfering Gluons.
An example of HERWIG configuration in the Config.C is shown below:
AliGenHerwig *gener = new AliGenHerwig(-1);
// final state kinematic cuts
gener->SetMomentumRange(0,7000);
gener->SetPhiRange(0. ,360.);
gener->SetThetaRange(0., 180.);
gener->SetYRange(-10,10);
gener->SetPtRange(0,7000);
// vertex position and smearing
gener->SetOrigin(0,0,0); // vertex position
gener->SetVertexSmear(kPerEvent);
gener->SetSigma(0,0,5.6); // Sigma in (X,Y,Z) (cm) on IP position
// Beam momenta
gener->SetBeamMomenta(7000,7000);
// Beams
gener->SetProjectile("P");
gener->SetTarget("P");
// Structure function
gener->SetStrucFunc(kGRVHO);
// Hard scatering
gener->SetPtHardMin(200);
gener->SetPtRMS(20);
// Min bias
gener->SetProcess(8000);
Generators for specific studies
MevSim
MevSim [31] was developed for the STAR experiment to quickly produce a large number of AA collisions for some specific needs; initially for HBT studies and for testing of reconstruction and analysis software. However, since the user is able to generate specific signals, it was extended to flow and event-by-event fluctuation analysis.
MevSim generates particle spectra according to a momentum model chosen by the user. The main input parameters are: types and numbers of generated particles, momentum-distribution model, reaction-plane and azimuthal-anisotropy coefficients, multiplicity fluctuation, number of generated events, etc. The momentum models include factorized pt and rapidity distributions, non-expanding and expanding thermal sources, arbitrary distributions in y and pt and others. The reaction plane and azimuthal anisotropy is defined by the Fourier coefficients (maximum of six) including directed and elliptical flow. Resonance production can also be introduced.
MevSim was originally written in FORTRAN. It was later integrated into AliRoot. A complete description of the AliRoot implementation of MevSim can be found on the web page (http://home.cern.ch/~radomski).
GeVSim
GeVSim is based on the MevSim event generator developed for the STAR experiment.
GeVSim is a fast and easy-to-use Monte Carlo event generator implemented in AliRoot. It can provide events of similar type configurable by the user according to the specific need of a simulation project, in particular, that of flow and event-by-event fluctuation studies. It was developed to facilitate detector performance studies and for the test of algorithms. GeVSim can also be used to generate signal-free events to be processed by afterburners, for example the HBT processor.
GeVSim generates a list of particles by randomly sampling a distribution function. The user explicitly defines the parameters of single-particle spectra and their event-by-event fluctuations. Single-particle transverse-momentum and rapidity spectra can be either selected from a menu of four predefined distributions, the same as in MevSim, or provided by user.
Flow can be easily introduced into simulated events. The parameters of the flow are defined separately for each particle type and can be either set to a constant value or parameterized as a function of transverse momentum and rapidity. Two parameterizations of elliptic flow based on results obtained by RHIC experiments are provided.
GeVSim also has extended possibilities for simulating of event-by-event fluctuations. The model allows fluctuations following an arbitrary analytically defined distribution in addition to the Gaussian distribution provided by MevSim. It is also possible to systematically alter a given parameter to scan the parameter space in one run. This feature is useful when analyzing performance with respect to, for example, multiplicity or event-plane angle.
HBT processor
Correlation functions constructed with the data produced by MEVSIM or any other event generator are normally flat in the region of small relative momenta. The HBT-processor afterburner introduces two particle correlations into the set of generated particles. It shifts the momentum of each particle so that the correlation function of a selected model is reproduced. The imposed correlation effects, due to Quantum Statistics (QS) and Coulomb Final State Interactions (FSI), do not affect the single- particle distributions and multiplicities. The event structures before and after the HBT processor are identical. Thus, the event reconstruction procedure with and without correlations is also identical. However, the track reconstruction efficiency, momentum resolution and particle identification are in general not identical, since correlated particles have a special topology at small relative velocities. We can thus verify the influence of various experimental factors on the correlation functions.
The method proposed by L. Ray and G.W. Hoffmann is based on random shifts of the particle three-momentum within a confined range. After each shift, a comparison is made with correlation functions resulting from the assumed model of the spacetime distribution and with the single- particle spectra that should remain unchanged. The shift is kept if the X 2- test shows better agreement. The process is iterated until satisfactory agreement is achieved. In order to construct the correlation function, a reference sample is made by mixing particles from consecutive events. Such a method has an important impact on the simulations, when at least two events must be processed simultaneously.
Some specific features of this approach are important for practical use:
- The HBT processor can simultaneously generate correlations of up to two particle types (e.g. positive and negative pions). Correlations of other particles can be added subsequently.
- The form of the correlation function has to be parameterized analytically. One and three dimensional parameterizations are possible.
- A static source is usually assumed. Dynamical effects, related to expansion or flow, can be simulated in a stepwise form by repeating simulations for different values of the spacetime parameters associated with different kinematic intervals.
- Coulomb effects may be introduced by one of three approaches:
- Gamow factor, experimentally modified Gamow correction and integrated Coulomb wave functions for discrete values of the source radii.
- Strong interactions are not implemented.
The detailed description of the HBT processor can be found elsewhere .
Flow afterburner
Azimuthal anisotropies, especially elliptic flow, carry unique information about collective phenomena and consequently are important for the study of heavy-ion collisions. Additional information can be obtained studying different heavy-ion observables, especially jets, relative to the event plane. Therefore it is necessary to evaluate the capability of ALICE to reconstruct the event plane and study elliptic flow.
Since a well understood microscopic description of the flow effect is not available so far, it cannot be correctly simulated by microscopic event
generators. Therefore, in order to generate events with flow, the user has to use event generators based on macroscopic models, like GeVSim or an afterburner which can generate flow on top of events generated by event generators based on the microscopic description of the interaction. In the AliRoot framework such a flow afterburner is implemented.
The algorithm to apply azimuthal correlation consists in shifting the azimuthal coordinates of the particles. The transformation is given by :

where v n (p t , y ) is the flow coefficient to be obtained, n is the harmonic number and Φ is the event-plane angle. Note that the algorithm is deterministic and does not contain any random number generation.
The value of the flow coefficient can either be constant or parameterized as a function of transverse momentum and rapidity. Two parameterizations of elliptic flow are provided as in GeVSim.
AliGenGeVSim* gener = new AliGenGeVSim(0);
Float_t mult = 2000; // Mult is the number of charged particles in |eta| < 0.5
Float_t vn = 0.01; // Vn
Float_t sigma_eta = 2.75; // Sigma of the Gaussian dN/dEta
Float_t etamax = 7.00; // Maximum eta
// Scale from multiplicity in |eta| < 0.5 to |eta| < |etamax|
Float_t mm = mult * (TMath::Erf(etamax/sigma_eta/sqrt(2.)) /
TMath::Erf(0.5/sigma_eta/sqrt(2.)));
// Scale from charged to total multiplicity
mm *= 1.587;
// Define particles
// 78% Pions (26% pi+, 26% pi-, 26% p0) T = 250 MeV
AliGeVSimParticle *pp = new AliGeVSimParticle(kPiPlus, 1, 0.26 * mm, 0.25, sigma_eta) ;
AliGeVSimParticle *pm = new AliGeVSimParticle(kPiMinus, 1, 0.26 * mm, 0.25, sigma_eta) ;
AliGeVSimParticle *p0 = new AliGeVSimParticle(kPi0, 1, 0.26 * mm, 0.25, sigma_eta) ;
// 12% Kaons (3% K0short, 3% K0long, 3% K+, 3% K-) T = 300 MeV
AliGeVSimParticle *ks = new AliGeVSimParticle(kK0Short, 1, 0.03 * mm, 0.30, sigma_eta) ;
AliGeVSimParticle *kl = new AliGeVSimParticle(kK0Long, 1, 0.03 * mm, 0.30, sigma_eta) ;
AliGeVSimParticle *kp = new AliGeVSimParticle(kKPlus, 1, 0.03 * mm, 0.30, sigma_eta) ;
AliGeVSimParticle *km = new AliGeVSimParticle(kKMinus, 1, 0.03 * mm, 0.30, sigma_eta) ;
// 10% Protons / Neutrons (5% Protons, 5% Neutrons) T = 250 MeV
AliGeVSimParticle *pr = new AliGeVSimParticle(kProton, 1, 0.05 * mm, 0.25, sigma_eta) ;
AliGeVSimParticle *ne = new AliGeVSimParticle(kNeutron, 1, 0.05 * mm, 0.25, sigma_eta) ;
// Set Elliptic Flow properties
Float_t pTsaturation = 2. ;
pp->SetEllipticParam(vn,pTsaturation,0.) ;
pm->SetEllipticParam(vn,pTsaturation,0.) ;
p0->SetEllipticParam(vn,pTsaturation,0.) ;
pr->SetEllipticParam(vn,pTsaturation,0.) ;
ne->SetEllipticParam(vn,pTsaturation,0.) ;
ks->SetEllipticParam(vn,pTsaturation,0.) ;
kl->SetEllipticParam(vn,pTsaturation,0.) ;
kp->SetEllipticParam(vn,pTsaturation,0.) ;
km->SetEllipticParam(vn,pTsaturation,0.) ;
// Set Direct Flow properties
pp->SetDirectedParam(vn,1.0,0.) ;
pm->SetDirectedParam(vn,1.0,0.) ;
p0->SetDirectedParam(vn,1.0,0.) ;
pr->SetDirectedParam(vn,1.0,0.) ;
ne->SetDirectedParam(vn,1.0,0.) ;
ks->SetDirectedParam(vn,1.0,0.) ;
kl->SetDirectedParam(vn,1.0,0.) ;
kp->SetDirectedParam(vn,1.0,0.) ;
km->SetDirectedParam(vn,1.0,0.) ;
// Add particles to the list
gener->AddParticleType(pp) ;
gener->AddParticleType(pm) ;
gener->AddParticleType(p0) ;
gener->AddParticleType(pr) ;
gener->AddParticleType(ne) ;
gener->AddParticleType(ks) ;
gener->AddParticleType(kl) ;
gener->AddParticleType(kp) ;
gener->AddParticleType(km) ;
// Random Ev.Plane
TF1 *rpa = new TF1("gevsimPsiRndm","1", 0, 360);
gener->SetPtRange(0., 9.) ; // Used for bin size in numerical
integration
gener->SetPhiRange(0, 360);
gener->SetOrigin(0, 0, 0); // vertex position
gener->SetSigma(0, 0, 5.3); // Sigma in (X,Y,Z) (cm) on IP position
gener->SetCutVertexZ(1.); // Truncate at 1 sigma
gener->SetVertexSmear(kPerEvent);
gener->SetTrackingFlag(1);
gener->Init();
Generator for e+e- pairs in PbPb collisions
In addition to strong interactions of heavy ions in central and peripheral collisions, ultra-peripheral collisions of ions give rise to coherent, mainly electromagnetic interactions among which the dominant process is the (multiple) e e -pair production :
AA -> AA + n(e +e -)
where n is the pair multiplicity. Most electronpositron pairs are produced into the very forward direction escaping the experiment. However, for Pb-Pb collisions at the LHC the cross-section of this process, about 230 kb, is enormous. A sizable fraction of pairs produced with large-momentum transfer can contribute to the hit rate in the forward detectors increasing the occupancy or trigger rate. In order to study this effect, an event generator for e e -pair production has been implemented in the AliRoot framework [38]. The class TEpEmGen is a realisation of the TGenerator interface for external generators and wraps the FORTRAN code used to calculate the differential cross-section. AliGenEpEmv1 derives from AliGenerator and uses the external generator to put the pairs on the AliRoot particle stack.
Combination of generators: AliGenCocktail
Different generators can be combined together so that each one adds the particles it has generated to the event stack via the AliGenCocktail class.

The AliGenCocktail generator is a realization of AliGenerator which does not generate particles itself but delegates this task to a list of objects of type AliGenerator that can be connected as entries (AliGenCocktailEntry) at run-time. In this way, different physics channels can be combined in one eve nt.
Here is an example of cocktail, used for studies in the TRD detector:
// The cocktail generator
AliGenCocktail *gener = new AliGenCocktail();
// Phi meson (10 particles)
AliGenParam *phi = new AliGenParam(10,new AliGenMUONlib(),AliGenMUONlib::kPhi,"Vogt PbPb");
phi->SetPtRange(0, 100);
phi->SetYRange(-1., +1.);
phi->SetForceDecay(kDiElectron);
// Omega meson (10 particles)
AliGenParam *omega = new AliGenParam(10,new AliGenMUONlib(),AliGenMUONlib::kOmega,"Vogt PbPb");
omega->SetPtRange(0, 100);
omega->SetYRange(-1., +1.);
omega->SetForceDecay(kDiElectron);
// J/psi
AliGenParam *jpsi = new AliGenParam(10,new AliGenMUONlib(), AliGenMUONlib::kJpsiFamily,"Vogt PbPb");
jpsi->SetPtRange(0, 100);
jpsi->SetYRange(-1., +1.);
jpsi->SetForceDecay(kDiElectron);
// Upsilon family
AliGenParam *ups = new AliGenParam(10,new AliGenMUONlib(), AliGenMUONlib::kUpsilonFamily,"Vogt PbPb");
ups->SetPtRange(0, 100);
ups->SetYRange(-1., +1.);
ups->SetForceDecay(kDiElectron);
// Open charm particles
AliGenParam *charm = new AliGenParam(10,new AliGenMUONlib(), AliGenMUONlib::kCharm,"central");
charm->SetPtRange(0, 100);
charm->SetYRange(-1.5, +1.5);
charm->SetForceDecay(kSemiElectronic);
// Beauty particles: semi-electronic decays
AliGenParam *beauty = new AliGenParam(10,new AliGenMUONlib(), AliGenMUONlib::kBeauty,"central");
beauty->SetPtRange(0, 100);
beauty->SetYRange(-1.5, +1.5);
beauty->SetForceDecay(kSemiElectronic);
// Beauty particles to J/psi ee
AliGenParam *beautyJ = new AliGenParam(10, new AliGenMUONlib(),
AliGenMUONlib::kBeauty,"central");
beautyJ->SetPtRange(0, 100);
beautyJ->SetYRange(-1.5, +1.5);
beautyJ->SetForceDecay(kBJpsiDiElectron);
// Adding all the components of the cocktail
gener->AddGenerator(phi,"Phi",1);
gener->AddGenerator(omega,"Omega",1);
gener->AddGenerator(jpsi,"J/psi",1);
gener->AddGenerator(ups,"Upsilon",1);
gener->AddGenerator(charm,"Charm",1);
gener->AddGenerator(beauty,"Beauty",1);
gener->AddGenerator(beautyJ,"J/Psi from Beauty",1);
// Settings, common for all components
gener->SetOrigin(0, 0, 0); // vertex position
gener->SetSigma(0, 0, 5.3); // Sigma in (X,Y,Z) (cm) on IP position
gener->SetCutVertexZ(1.); // Truncate at 1 sigma
gener->SetVertexSmear(kPerEvent);
gener->SetTrackingFlag(1);
gener->Init();