The delta-transformation is the transformation which defines the displacement to be applied to the given physical volume. During offline alignment we want to correct the hard-coded, ideal position of some volumes, initially fixed according to the engeneers'drawings, by including the survey and alignment information related to those volumes; we say that we want to align the ideal geometry. With this aim, we need here to describe how the delta-transformations are defined and thus how they have to be produced and applied to the ideal geometry in order to correct the global and local ideal transformations into global and local aligned transformations.

For the representation of the delta-transformation there are several possible conventions and choices, in particular:

1. the use of local-to-global or global-to-local convention and active or passive transformations convention;
2. the use of local or global delta-transformation to be stored in the alignment object and to be passed when setting the object itself;
3. the convention used for the Euler angles representing the delta-transformation;
4. the use of a matrix or of a minimal set of parameters (three orthogonal shifts plus three Euler angles) to be stored in the alignment object and to be passed when setting the object itself.

The choices adopted by the framework are explained in the following:

Global and local delta-transformations

Being based on the ROOT geometry package (TGeo), the AliRoot offline alignment framework derives from TGeo the basic conventions for the representation of a generic transformation: therefore we recall them here.  TGeo uses transformations both for positioning a volume inside another one (mother volume) and for converting vectors between the two RSs. TGeo represents each transformation as a homogeneous transformation in the "local to global" convention. The transformation is used both for defining the placement of a volume with respect to its container reference frame and for converting vectors between the volume RS and the mother volume RS. The "local to global" convention means that applying the matrix to the vector in the local RS one gets the vector in the mother RS, while the inverse of the transformation converts a global vector into a local one. The general homogenous transformation embeds a rotation, a translation and a scale. Using transformation matrices containing homogeneous coordinates, TGeo can seamlessly intermix translations with all other types of transformations; the drawbacks are the need to deal with 4x4 matrices (in a 3D space) and the fact that even the composition of two translations results in a matrix product.
We clarify the explanation with an example, where the transformation includes a rotation and a translation, but no scale (by far the most common case): let

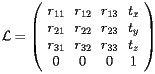(1)

 
be the matrix used for positioning the volume B inside its mother volume A . In this example 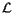has a rotational part 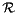and a translational part :

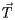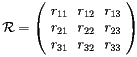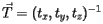(2)

Let now 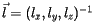be a vector defined in the RS associated to volume B; 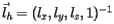is then the 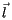vector expressed as a homogenous vector.

Then 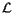performs the "local to master" conversion, i.e. the homogeneous vector 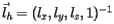in the local RS of volume B is transformed in the corresponding homogeneous vector 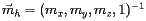in the mother RS of volume A by:

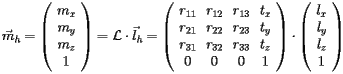(3)

For the corresponding 3D vectors the equivalent transformation is expressed by:

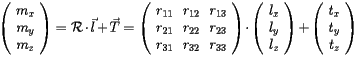(4)

From the equation above one can see that the translation is applied after the rotation.
Let us from now on drop the h subscript, being clear from the context wheter we refer to normal or homogeneous vectors.
The transformation 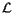which transforms a local vector 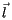into the corresponding vector in the mother volume RS, 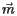, according to:

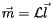(6)

is called the local transformation. If furthermore 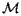is the global transformation for the mother volume (transforming from the mother volume RS to the global RS), then we can write:

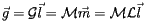(7)

Recursively repeating this argument to all the parent volumes, that is to all the volumes in the branch of the geometry tree which contains the given volume, we can write:

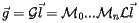(8)

This means that the global transformation for a given volume is the matrix 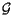which, as in TGeo, transforms the local vector 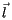(giving the position in the local reference system, i.e. the reference system associated to that volume) into the global vector 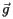, giving the position in the global (or master) reference system ("MARS"), according to:

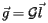(5)

This shows that the global matrix for the given volume is given by the pile-up of all local transformations in the branch of the geometry tree containing the given volume, from the uppermost to the lowest level.

Let's now say that the matrices 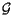and 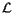which appear in Eqs.  (5)- (8) are the global and local ideal matrices, that is the reference matrices giving the hard-coded positions for the given volume initially fixed by the AliDET::CreateGeometry methods. Let's also put the superscript ' 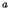' to the corresponding matrices in the aligned geometry, so that 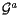and 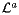are the aligned global and aligned local transformations which relate the position of a point in the local RS to its position in the global RS and in the mother's RS respectively, after the volume has been aligned, according to:

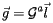	(9)
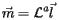	(10)

which are the equations corresponding to Eqs.  (5) and (6) after the volume has been aligned.

There are two possible choices for expressing the delta-transformation; either we use:

• the global delta-transformation 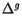, that is the transformation to be applied to the ideal global transformation 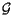in order to get the aligned global transformation:
  

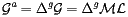
  (11)

• the local delta-transformation 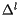, that is the transformation to be applied to the ideal local transformation to get the aligned local transformation:
  

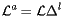
  (12)

Eqs.  (11) and (12) allow to rewrite:

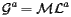(13)

as:

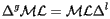(14)

or equivalently:

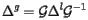	(15)
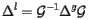	(16)

to relate global and local alignment.

The alignment object stores as delta-transformation the global delta-transformation; nevertheless both global and local delta-transformations can be used to construct the alignment object or to set it. The reasons for including this flexibility in the user interface is that the local RS is sometimes the most natural one for expressing the displacement, as e.g. in the case of a volume rotated around its centre. However the use of the local delta-transformation is sometimes error-prone; in fact the user has to be aware that he is referring to the same local RS which is defined in the hard-coded geometry when positioning the given volume, while the local RS used by simulation or reconstruction code can in general be different. In case the alignment object is constructed or its delta-transformation is set by means of the local delta-transformation, the framework will then use Equation  (14) to perform the conversion into global alignment constants.

Matrix or parameters to represent the transformation

The global delta-transformation can be saved both

• as a TGeoHMatrix and
• as a set of six parameters, out of which three define the translation, being the shifts in the three orthogonal directions, and three define the rotation, being the three Euler angles describing it.

This two cases correspond to choosing one of the following two AliAlignObj -derived classes:

• AliAlignObjMatrix : stores a TGeoHMatrix
• AliAlignObjParams : stores six double precision floating point numbers;

While storing the alignment constants in a different form, they appear with the same user interface, which allows to set the delta-transformation both via the matrix and via the six parameters which identify it.

Convention for the Euler angles

A general rotation in three-dimensional Euclidean space can be decomposed into, and represented by, three successive rotations about the three orthogonal axis. The three angles characterising the three rotations are called Euler angles; however there are several conventions for the Euler angles, depending on the axes about which the rotations are carried out, right/left-handed systems, (counter)clockwise direction of rotation, order of the three rotations.

The convention chosen in the ALICE alignment framework for the Euler angles is the " xyz convention", also known as pitch-roll-yaw or Tait-Bryan angles, or Cardano angles convention. Following this convention the general rotation is represented as a composition of a rotation around the z-axis (yaw) with a rotation around the y'-axis (pitch) with a rotation around the x''-axis (roll) - where (x,y,z),(x',y',z') and (x'',y'',z'')are the original RS and the RS after the first and second rotation respectively. The picture below shows the three rotations which transform the original system, (x,y,z) in black, into the final coordinate system (X,Y,Z) in blue, passing through the intermediate steps, (x',y',z') in red and (x'',y'',z'') in green.

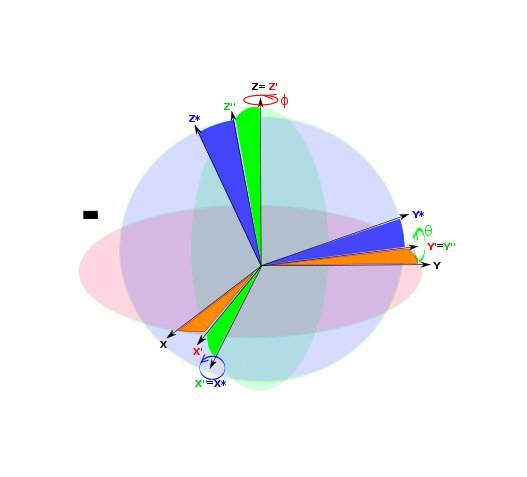
There is an additional choice to fully specify the convention used, since the angles have opposite sign whether we consider them as bringing the original RS in coincidence with the aligned RS ("active-transformation" convention) or as bringing the vectors in the original RS in coincidence with those in the aligned RS ("passive-transformation" convention). In order to maintain our representation fully consistent with the TGeo interface, we choose the "active-transformation" convention; in this way our euler angles are according to the pitch-roll-yaw angles convention referenced above, but for the sign which is the opposite.

To summarise, the three angles - 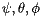- used by the framework to represent the rotation part of the delta-transformation, unambiguously represent a rotation 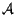as the composition of the following three rotations:

1. a rotation 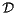by an angle 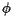(yaw) around the z-axis
   

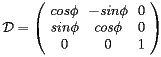
   (17)

2. a rotation 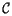by an angle 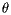(pitch) around the y-axis
   

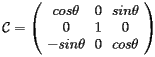
   (18)

3. a rotation by an angle (roll) around the x-axis
   

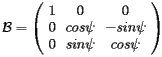
   (19)

which leads to:

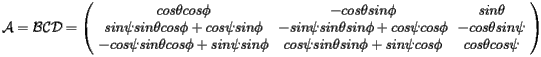(20)

In the case of alignment the rotations to be applied are usually very small; in this case we can approximate the sins by the angles and the cosines by 1 and the final expression for the rotation matrix 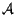is:

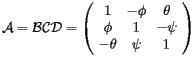(21)

To summarise, the ALICE alignment framework fixes the following conventions concerning the delta-transformation:

• the transformations are interpreted according to the local-to-global convention
• the delta-transformation stored is the global delta-transformation
• the three parameters to specify the rotation are the roll-pitch-yaw Euler angles, with the "active transformations" convention.

The interface still leaves several choices to the user, who:

• can choose to set the alignment object either by passing a TGeoMatrix or by giving the six parameters which uniquely identify the global delta-transformation;
• can choose if he wants the object to store either the TGeoHMatrix , using an AliAlignObjMatrix or the six parameters, using an AliAlignObjParams ;
• can choose if the transformation he is passing is the global delta-transformation or the local delta-transformation; in this latter case the framework converts it to the global one to set the internal data members.